Summary

This example shows how to create a complete mortgage payment schedule with a single formula. It features several new dynamic array functions including LET, SEQUENCE, SCAN, LAMBDA, VSTACK, and HSTACK. It also uses a number of traditional financial functions including  PMT, IPMT, PPMT, and SUM. The resulting table spans columns E to I and includes 360 rows, one for each monthly payment for the entire 30-year loan term.

Note: this formula was suggested to me by Matt Hanchett, a reader of Exceljet's newsletter. It is an excellent example of how Excel's new dynamic array formula engine can be used to solve complicated problems with a single formula. Requires Excel 365 for now.

Explanation 

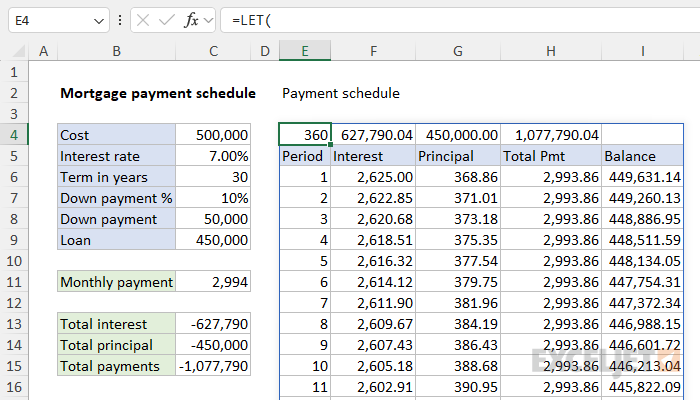
In this example, the goal is to generate a basic mortgage payment schedule. A mortgage payment schedule is a detailed breakdown of all the payments you will make over the life of a mortgage. It provides a chronological list of each payment, showing the amount that goes toward the principal (the loan amount), the amount that goes toward interest, and the balance that remains.  The schedule provides a clear picture of how the loan will progress over time. It shows how payments early in the loan go mainly toward interest payments while payments near the end of the loan go mainly toward paying off the principal.

This article explains two approaches, (1) a single formula solution that works in Excel 365, and (2) a more traditional approach based on several different formulas for older versions of Excel. A key goal is to create a dynamic schedule that automatically updates when the loan term changes. Both approaches build on the example here for estimating a mortgage payment.

This simplified example ignores property taxes, homeowner's insurance, mortgage insurance, and other fees.

Single formula

The single formula option requires Excel 365. In the worksheet shown above, we are generating the entire mortgage schedule with a single dynamic array formula in cell E4 that looks like this:

=LET(
loanAmt,C9,
intAnnual,C5,
loanYears,C6,
rate,intAnnual/12,
nper,loanYears*12,
pv,-loanAmt,
pmt,PMT(rate,nper,pv),
pers,SEQUENCE(nper),
ipmts,IPMT(rate,pers,nper,pv),
ppmts,PPMT(rate,pers,nper,pv),
bals,SCAN(loanAmt,ppmts,LAMBDA(x,r,x-r)),
tInterest,SUM(ipmts),
tPrincipal,SUM(ppmts),
tPaid,tInterest+tPrincipal,
VSTACK(
HSTACK(nper,tInterest,tPrincipal,tPaid,""),
HSTACK("Period","Interest","Principal","Total Pmt","Balance"),
HSTACK(pers,ipmts,ppmts,ipmts+ppmts,bals)
))

At a high level, this formula calculates and displays a mortgage payment schedule, detailing the number of periods (months), interest payment, principal payment, total payment, and remaining balance for each period based on the given loan details.

LET function

The LET function is used to define named variables that can be used in subsequent calculations. This makes the formula more readable and eliminates the need to repeat calculations. The LET function defines the variables used in the formula as follows:

  • loanAmt: Amount of the loan (C9).
  • intAnnual: Annual interest rate (C5).
  • loanYears: Total years of the loan (C6).
  • rate: Monthly interest rate (annual interest rate divided by 12).
  • nper: Total number of payment periods (loan term in years multiplied by 12).
  • pv: Present value of the loan, which is the negative of the loan amount.
  • pmt: The monthly payment, which is calculated with the PMT function.
  • pers: All periods, a dynamic array of numbers from 1 to nper using the SEQUENCE function.
  • ipmts: Interest payments for each period, calculated with the IPMT function.
  • ppmts: Principal payments for each period, calculated with the PPMT function.
  • bals: Remaining balances for each period, calculated with the SCAN function and the LAMBDA function to sequentially subtract the principal payment from the initial loan amount.
  • tInterest: The total interest paid over the term.
  • tPrincipal: The total principal paid over the term.
  • tPaid: The total of all payments made over the term.

Most of the calculations above are straightforward, but it's worth pointing out that because nper is 360 (30 years * 12 months per year), and because nper is provided to SEQUENCE:

  • The SEQUENCE function returns 360 periods.
  • The IPMT function returns 360 interest payments.
  • The PPMT function returns 360 principal payments.
  • The SCAN function returns a running balance with 360 entries.

In other words, this is the core of the dynamic formula. Each of these operations returns an entire column of data for the final payment schedule.

VSTACK and HSTACK

The variables defined above are assembled into a final layout with the  VSTACK function and the HSTACK function:

VSTACK(
HSTACK(nper,tInterest,tPrincipal,tPaid,""),
HSTACK("Period","Interest","Principal","Total Pmt","Balance"),
HSTACK(pers,ipmts,ppmts,ipmts+ppmts,bals)
)

Working from the inside out, the HSTACK function stacks arrays or ranges side by side horizontally. HSTACK is used here to:

  • Assemble the values that appear in the total row in E4:I4.
  • Assemble the table header that appears in the range E5:I5.
  • Assemble the columns of data created earlier, including the periods, interest payments, principal payments, total payments, and the remaining balance for each period.

Notice that HSTACK runs inside the VSTACK function, which combines ranges or arrays in a vertical fashion. In this case, VSTACK combines the output from each separate HSTACK function vertically in the order shown above.

Option for older versions of Excel

In older versions of Excel (Excel 2019 and older) we can't create the payment schedule with a single formula because dynamic arrays are not supported. However, it is still possible to build out the mortgage payment schedule one formula at a time. This is the approach demonstrated on Sheet2 of the attached workbook. First, we define three named ranges:

  • IntAnnual - the interest rate in C5
  • loanAmt - the loan amount in C9
  • loanYears - the years in C6

Then, in the range E6:I6 we use the following formulas:

E6=1 // period 1 hardcoded
F6=IPMT(intAnnual/12,E6,loanYears*12,-loanAmt) // interest
G6=PPMT(intAnnual/12,E6,loanYears*12,-loanAmt) // principal
H6=F6+G6 // total payment
I6=loanAmt-G6 // balance

In order to make the term in years variable, we need to do some extra work in the formulas. Namely, we need to stop the periods from incrementing when we reach the total number of periods (term * 12) and then suppress the other calculations after that point. We do this by incorporating some extra logic. First, we check to see if the previous period is less than the total periods for the entire loan (loanYears * 12). If so, we increment the previous period by 1. If not, we are done and return an empty string:

E7=IF(E6<loanYears*12,E6+1,"")

The next remaining formulas check to see if the period number in the same row is a number before calculating a value:

F7=IF(ISNUMBER(E7),IPMT(intAnnual/12,E7,loanYears*12,-loanAmt),"")
G7=IF(ISNUMBER(E7),PPMT(intAnnual/12,E7,loanYears*12,-loanAmt),"")
H7=IF(ISNUMBER(E7),F7+G7,"")
I7=IF(ISNUMBER(E7),I6-G7,"")

The result of this extra logic is that if the term is changed to say, 15 years, the extra rows in the table after 15 years will appear blank. The named ranges are used to make the formulas easier to read and to avoid a lot of absolute references. To study these formulas in detail, download the workbook and have a look at Sheet2.

Related formulas

Excel formula: Estimate mortgage payment

Estimate mortgage payment

In this example, the goal is to calculate a monthly mortgage payment based on three inputs: The loan amount The annual interest rate The loan term in years The worksheet shown also takes into account the down payment, which is calculated using a simple formula in C8 (see below) and then subtracted...
Excel formula: Calculate payment for a loan

Calculate payment for a loan

Loans have four primary components: the amount, the interest rate, the number of periodic payments (the loan term) and a payment amount per period. You can use the PMT function to get the payment when you have the other 3 components. For this example, we want to find the payment for a $5000 loan...

Related functions

Excel LET function

LET Function

The Excel LET function lets you define named variables in a formula. There are two primary reasons you might want to do this: (1) to improve performance by eliminating redundant calculations and (2) to make more complex formulas easier to read and write....
Excel SEQUENCE function

SEQUENCE Function

The Excel SEQUENCE function generates a list of sequential numbers in an array. The array can be one dimensional, or two-dimensional, determined by rows and columns arguments. 
Excel SCAN function

SCAN Function

The SCAN function applies a custom calculation to each element in a given array or range and returns an array that contains the intermediate values created during the scan. SCAN can be used to generate running totals, running counts, and other calculations...
Excel PMT function

PMT Function

The Excel PMT function is a financial function that returns the periodic payment for a loan. You can use the PMT function to figure out payments for a loan, given the loan amount, number of periods, and interest rate.
Excel IPMT function

IPMT Function

The Excel IPMT function is a financial function used to calculate the interest payment for a given period of an investment or a loan, based on constant periodic payments and a constant interest rate. For example, you can use IPMT to get the interest amount of a loan payment for the...
Excel PPMT function

PPMT Function

The Excel PPMT function can be used to calculate the principal portion of a given loan payment. For example, you can use PPMT to calculate the principal amount of a payment for the first period, the last period, or any period in between.
Excel HSTACK function

HSTACK Function

The Excel HSTACK function combines arrays horizontally into a single array. Each subsequent array is appended to the right of the previous array....
Excel VSTACK function

VSTACK Function

The Excel VSTACK function combines arrays vertically into a single array. Each subsequent array is appended to the bottom of the previous array....
Dave Bruns Profile Picture

AuthorMicrosoft Most Valuable Professional Award

Dave Bruns

Hi - I'm Dave Bruns, and I run Exceljet with my wife, Lisa. Our goal is to help you work faster in Excel. We create short videos, and clear examples of formulas, functions, pivot tables, conditional formatting, and charts.

Formulas

Functions

Training