Explanation
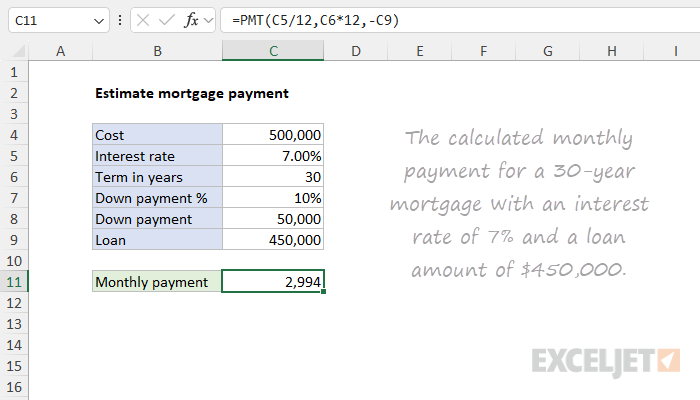
In this example, the goal is to calculate a monthly mortgage payment based on three inputs:
- The loan amount
- The annual interest rate
- The loan term in years
The worksheet shown also takes into account the down payment, which is calculated using a simple formula in C8 (see below) and then subtracted from the cost in cell C4. The mortgage payment is then calculated based on the loan amount in cell C9.
This simplified example ignores property taxes, homeowner's insurance, mortgage insurance, and other fees.
Mortgages and interest calculations
A mortgage is a type of loan specifically used to purchase real estate. In a mortgage agreement, the buyer borrows money from a lender to buy a home and repays the loan over a long period of time. Here are the main components:
- Principal - The total loan amount, after any down payment.
- Interest - The cost of borrowing money. The lender charges a percentage of the principal amount as interest. This interest is usually compounded on a monthly basis for mortgages over the entire term.
- Term - This is the number of years you have to pay back the loan. Common terms for mortgages are 15, 20, or 30 years.
The monthly mortgage payment is made up of both the principal and the interest. Over time, a larger portion of the monthly payment goes toward reducing the loan balance (or principal), and a smaller portion goes toward paying interest.
The PMT function in Excel
The PMT function in Excel calculates the monthly payment for a loan, given the loan amount, interest rate, and repayment time. The PMT function assumes fixed periodic payments and a constant interest rate. The full generic syntax for PMT looks like this
=PMT(rate,nper,pv,[fv],[type])
Each argument has the following meaning:
- rate: The interest rate for the loan.
- nper: The total number of payment periods for the loan.
- pv: The principal amount of the loan.
- fv (optional): The cash balance desired after the last payment is made. Defaults to 0.
- type (optional): When payments are due (0 = end of period, 1 = beginning of period). Defaults to 0.
Although the PMT function takes five arguments total, we only need the first three arguments (rate, nper, and pv) to estimate the mortgage payment in this example.
Example
You can use the PMT function to calculate the payment for a mortgage by providing the interest rate, the term, and the loan amount. In the example shown, the formula in cell C11 is:
=PMT(C5/12,C6*12,-C9)
The arguments are provided to PMT as follows:
- rate = C5/12 (7%/12)
- nper = C6*12 (30*12)
- pv = -C9 (-450000)
Because mortgage rates are annual, and terms are stated in years, the arguments for the rate and periods are carefully set up to normalize inputs to monthly periods. To get the rate (which is the period rate), we divide the annual rate (7%) by the compounding periods per year (12). To get the number of periods (nper), we multiply the term in years (30) by the periods per term (12). To get a value for pv (the present value), we use -C9, which converts the loan amount to -450,000. We use a minus operator to make this value negative, since a loan represents money owed, and is a cash outflow. Putting it all together, Excel evaluates the formula like this:
=PMT(C5/12,C6*12,-C9)
=PMT(0.07/12,30*12,-450000)
=PMT(0.005833,360,-450000)
=2994
The PMT function returns 2,994. This is the calculated monthly payment for a 30-year mortgage with an interest rate of 7% and a loan amount of $450,000.
Note: When using PMT, always be consistent with the units provided for rate and periods. For a mortgage, you typically need to divide the annual interest rate by 12 to get a period rate and multiply the term by 12 to get the total number of periods.
Other worksheet formulas
The worksheet shown contains two other formulas. In the first formula, the down payment amount in C8 is calculated like this:
=C4*C7
This formula multiples the cost in C4 by the down payment percentage in C7. With $500,000 in cell C4 and 10% in cell C7, the down payment is calculated to be $50,000. In the second formula, the loan amount in C9 is calculated like this:
=C4-C8
This formula subtracts the down payment in C8 from the cost in C4 to determine a loan amount. With $500,000 in cell C4 and $50,000 in C8, the result in C9 is $450,000.
Note: the interest rate in C5 and the down payment percentage in C7 are decimal values formatted with Excel's percentage number format.