Purpose
Return value
Syntax
=PV(rate,nper,pmt,[fv],[type])- rate - The interest rate per period.
- nper - The number of payment periods.
- pmt - The payment made each period.
- fv - [optional] Future value. If omitted, defaults to zero.
- type - [optional] Payment type, 0 = end of period, 1 = beginning of period. Default is 0.
Using the PV function
The PV function returns the value in today's dollars of a series of future payments, assuming periodic, constant payments and a constant interest rate. You can use the PV function to calculate the present value of a loan or investment when the interest rate and cash flows are constant. The PV function takes five separate arguments, three of which are required as explained below.
rate (required) - the interest rate per period. For example, if the annual interest rate is 6% and periods are monthly, then the interest rate is =6%/12 = 0.5% (0.005). You can enter the rate as 6%/12 as a reminder of how it is derived.
nper (required) - The total number of payment periods in the annuity. For example, a 5-year car loan with monthly payments has 60 periods. You can enter nper as 5*12 to note how the number was determined.
pmt (required) - The payment made each period. This number cannot change over the life of the annuity. In annuity functions, cash paid out is represented by a negative number. Note: If pmt is not provided, the optional fv argument must be supplied.
fv (optional) - The future value. This is the cash balance required after all payments have been made. When fv is omitted, it defaults to zero, and pmt must be supplied.
type (optional) - type is a boolean that controls when payments are due. Supply 0 for payments due at the end of the period (regular annuities) and 1 for payments due at the end of the period (annuities due). Type defaults to 0 (end of period).
Examples
The PV function can be used to calculate the present value of a loan, when the interest rate, payment, and number of periods are known. For example, the present value of a 5-year loan with an annual interest rate of 4.5% and monthly payments of $93.22 is approximately $5,000:
=PV(4.5%/12,5*12,-93.22) // returns 5000.26
In the worksheet shown above, the formula in C10 is:
=PV(C5/C8,C7,C6)
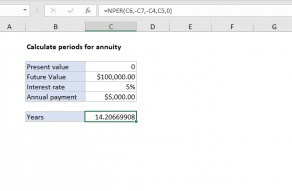
Present value of annuity
To calculate the present value of an annuity that pays 10,000 per year for 25 years, with an annual interest rate of 7%:
=PV(7%,25,10000) // returns -116,535.832
To return a positive present value, enter the payment as a negative number:
=PV(7%,25,-10000) // returns 116,535.832
Also, see Present value of an annuity.
Investment goal
To calculate the initial investment required to reach $15,000 in 10 years with an annual interest rate of 5%:
=PV(5%,10,0,15000) // returns -9,208.70
Enter the future value as a negative number to get a positive result:
=PV(5%,10,0,-15000) // returns 9,208.70
PV versus NPV
Both the PV function and the NPV function calculate present value, but there are differences in the way they operate:
- The PV function can only be used when cash flows are constant and don't change. The NPV function can be used to calculate the present value of uneven cash flows spaced evenly in time.
- The PV function has a type argument to handle regular annuities and annuities due. The NPV function always assumes a regular annuity, where payments are due at the end of the period.
Notes
- A stream of cash flows that includes the same amount of cash outflow (or inflow) each period is called an annuity. For example, a car loan or a mortgage is an annuity. When each period's interest rate is the same, an annuity can be valued using the PV function.
- In annuity functions, the cash you pay out (such as a deposit to savings) is represented by a negative number; cash you receive, such as a dividend check, is represented by a positive number. For a $2,500 deposit to a bank, the pmt would be -2500 if you are the depositor, and 2500 if you are the bank.