Purpose
Return value
Syntax
=IPMT(rate,per,nper,pv,[fv],[type])- rate - The interest rate per period.
- per - The given payment period.
- nper - The total number of payment periods.
- pv - The present value, or total value of all payments now.
- fv - [optional] The cash balance desired after last payment is made. Defaults to 0.
- type - [optional] When payments are due. 0 = end of period. 1 = beginning of period. Default is 0.
Using the IPMT function
The IPMT function returns the interest payment for a given payment period of an investment or a loan, based on constant periodic payments and a constant interest rate. IPMT takes six arguments, four of which are required:
=IPMT(rate,per,nper,pv,[fv],[type])
Each argument has the following meaning:
- rate - the interest rate per period. Typically, this is the annual interest rate divided by the compounding periods per year.
- per - the payment period of interest as a number (e.g. 1, 2, 3, etc.)
- nper - The total number of payment periods for the loan or investment.
- pv - The present value, or the principal amount of the loan or investment.
- fv - Optional. The desired future value, or a cash balance after the last payment (defaults to 0)
- type - Optional. The timing of the payment: 0 = end of period (default), 1 = beginning of the period.
Example #1 - hardcoded values
Suppose you have a 5-year loan of $10,000 with an annual interest rate of 5% and 12 compounding periods per year. You want to find out the amount of interest paid in period 1. You can determine this amount with the IPMT function like this:
=IPMT(5%/12,1,60,-10000)
The inputs to IPMT are as follows:
- rate - 5%/12 = 0.00416 (annual interest rate with monthly compounding)
- per - 1 (interest for period 1)
- nper - 60 (a 5-year loan has 60 periods)
- pv - -10,000 (the loan amount is negative to yield a positive result)
- fv - Omitted. Defaults to 0.
- type - Omitted. Defaults to 0.
The result is 41.67. This is the interest payment for period 1 of the loan. Notice we have provided the loan balance as a negative value to get a positive result from IPMT. If we provide 10,000 as a positive number, IPMT will return -41.67. The decision to use a positive or negative value for pv depends on the specific scenario.
Example #2 - worksheet formula
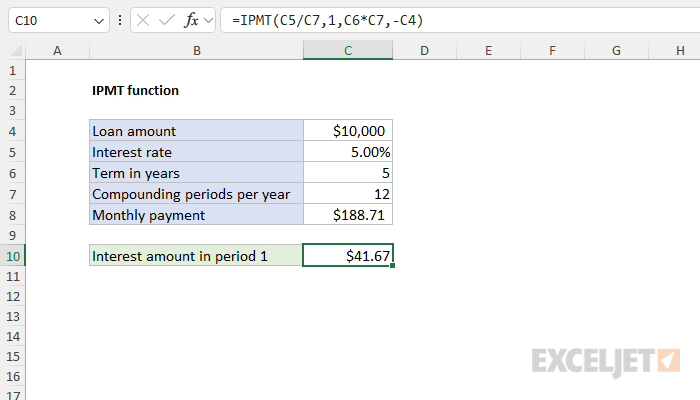
In the example above, all inputs to IPMT are hardcoded to make the formula easier to read. More typically, the inputs will come from cell references. The screen below shows how the same example can be transferred to a worksheet:

The formula in cell C10 is evaluated like this:
=IPMT(C5/C7,1,C6*C7,-C4)
=IPMT(0.05/12,1,5*12,-10000)
=IPMT(0.004167,1,60,-10000)
41.67
Notice that we provide years * periods per year for nper instead of hardcoding the number 60. We do this so that the formula will automatically adapt to a loan with a different term in years, or a loan with a different number of periods per year.
Also, notice that the monthly payment is not an input to IPMT. This is because IPMT calculates interest based on the original principal (or present value), the interest rate, and the number of periods. The payment amount isn't needed. To calculate the payment for a loan you can use the PMT function.
Notes
- Use the PPMT function to get the principal portion of a loan payment for a given period.
- The interest rate can be provided as a percentage like 5% or a decimal number like 0.05.
- Be careful to provide the periodic interest rate for rate. For example, 5%/12 or 0.05/12.
- The loan value (pv) can be entered as a positive value or a negative value.
- The value for period (per) must be in the range 1 to nper.