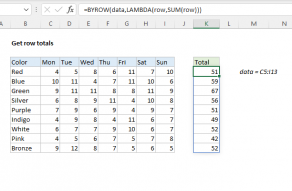
Explanation
In this example, the goal is to return an array with 7 subtotals, one for each day of the week, as seen in columns C:I. The numbers to sum are contained in data which is the named range C5:I13. This is an example of a problem where the goal is to create an array of sums rather than a single sum. We can't use a function like SUM by itself, because SUM will aggregate results and return a single value. In the article below, we look at two approaches, one based on the BYCOL function, and one based on the MMULT function.
With the BYCOL function
In Excel 365, the most straightforward way to generate subtotals for each column is with the BYCOL function. The purpose of BYCOL is to process data in a "by column" fashion. For example, if BYCOL is given an array with 7 columns, BYCOL will return single array with 7 results. In the example shown, the formula in C15 is:
=BYCOL(data,LAMBDA(col,SUM(col)))
The calculation performed on each column is provided by a custom LAMBDA function, which must return a single result for each column. In this example, the LAMBDA function used in BYCOL sums each row like this:
LAMBDA(col,SUM(col)) // sum each column
The result is an array of sums, one per column, that spill into the range C15:I15. This result is fully dynamic. If data values change, or if the data range expands or contracts, the output from BYCOL will update as needed.
The result is an array of sums, one per row, that spill into the range K5:K13. This result is fully dynamic. If data values change, or if the data range expands or contracts, the output from BYROW will update as needed. Although this example deals with totals, the same pattern can be used to calculate other information about columns, including max, min, average, etc. like this:
=BYCOL(data,LAMBDA(col,MAX(col))) // max
=BYCOL(data,LAMBDA(col,MIN(row))) // min
=BYCOL(data,LAMBDA(col,AVERAGE(col))) // average
With the MMULT function
Another way to solve this problem is with the MMULT function, which performs matrix multiplication. MMULT takes two arrays, array1 and array2, and requires that the number of columns in array1 be the same as the number of rows in array2. The resulting matrix will have same number of rows as the first matrix, and the same number of columns as the second matrix. The MMULT formula looks like this:
=MMULT(TRANSPOSE(ROW(data)^0),--data)
In column-based operations with MMULT, the data appears as array2, which is simply all values in data, the named range C5:I13:
--data
To protect against blank cells, which will cause MMULT to throw #VALUE! error, we use a double negative (--) to force any empty cells to zero.
Array1 needs to be constructed with respect to array2. Because array2 contains 9 rows, we need array1 to contain 9 columns. We want just a single row of results, so the dimensions of array1 should be 1 row by 9 columns (1 x 9). Also, because we don't want to change any values, array1 should contain only the number 1 (i.e. multiplying by 1 does not change the original value). The code to create array1 uses the TRANSPOSE function and the ROW function like this:
TRANSPOSE(ROW(data)^0)
The ROW function returns a 1 x 7 array of row numbers:
ROW(data) // returns {5;6;7;8;9;10;11;12;13}
Next, these numbers are raised to the power of zero with exponent operator (^), which creates a 1 x 7 array of 1s:
ROW(data)^0) // returns {1;1;1;1;1;1;1;1;1}
And the TRANSPOSE function flips the array from 9 x 1 to 1 x 9:
TRANSPOSE({1,1,1,1,1,1,1}) // returns {1,1,1,1,1,1,1,1,1}
The result is handed off to the MMULT function as array1. The MMULT function then performs matrix multiplication with the two arrays, and returns a subtotal for each row:
=MMULT({1,1,1,1,1,1,1,1,1},--data)
returns the array:
{59,77,67,68,69,72,67}
These values are returned to cell C15, and spill into the range C15:I15.
SEQUENCE alternative
Another way to construct array1 inside MMULT is with the SEQUENCE function like this:
=MMULT(SEQUENCE(1,ROWS(data),1,0),--data)
This formula works the same way, but array1 is created with the SEQUENCE function directly:
SEQUENCE(1,ROWS(data),1,0)
Note we use the ROWS function to tell SEQUENCE how many columns to create (7).