Modeling the 4 Percent Retirement Rule in Excel

The 4% retirement rule suggests you can safely withdraw 4% of your portfolio in year one of retirement, then adjust that amount for inflation each year for 30 years without running out of money. But how does this actually play out year by year? This article builds a complete Excel model to find out, exploring three different approaches, from classic row-by-row formulas to modern dynamic arrays to a single formula that generates the entire 30-year schedule. These models are fully functional, so you can play with the inputs and see how things work yourself.

What is the 4% retirement rule?
How the 4% rule works
What we need to model in Excel
The model in Excel
Traditional approach (Sheet1)
Hybrid approach (Sheet2)
Single formula approach (Sheet3)
Summary and conclusion
Functions used in the workbook
Instructions

What is the 4% retirement rule?

If you look into retirement planning, you'll probably run into the 4% retirement rule, one of the most well-known (and frequently cited) guidelines for retirement spending. In brief, the 4% retirement rule tries to answer this question in a simple way: "How much can I safely withdraw from my retirement savings each year without running out of money?" The answer? About 4%, adjusted for inflation.

The rule came out of research conducted by a financial advisor named Bill Bengen in 1994. His goal was to determine a safe withdrawal rate (SAFEMAX) that would allow retirees to maintain their standard of living throughout a 30-year retirement without running out of money, even across periods of poor market performance and high inflation.

Based on a historical reconstruction of retiree portfolios since 1926, Bengen recommended a 4% withdrawal rate for the first year, followed by cost-of-living adjustments each succeeding year. Although Bengen himself didn't refer to a "4% rule" (and later changed his recommendation to 4.5% and then to 4.7%), the name stuck and carries on to this day.

How the 4% rule works

Applying the rule is simple: in your first year of retirement, you withdraw 4% of your total portfolio balance. In each subsequent year, you adjust that initial dollar amount for inflation rather than recalculating 4% of your current balance. For example, if you retire with a $1 million portfolio, you would withdraw $40,000 in year one. If inflation is 3% that year, you'd withdraw $41,200 in year two, and so on. The idea is to provide predictable, inflation-adjusted income while preserving the portfolio across various market conditions across the entire retirement period.

For those planning retirement, the 4% rule serves as both a withdrawal strategy and a savings target. If you know your desired annual retirement income, you can work backward to determine how much you need to save: simply multiply your target income by 25 (since 4% × 25 = 100%). While the rule has plenty of critics and may need adjustment based on individual circumstances, it remains a useful starting point for retirement planning. It is also a great example of a problem that can be modeled in Excel, where you can easily test various scenarios and assumptions.

I’m not a financial advisor. My goal is not to convince you that the 4% rule is the best way to plan for retirement. My goal is to show how you can model a problem like this in Excel in different ways.

What we need to model in Excel

Before we get into details, let's review what we need to model: Beginning with a given starting balance (total retirement savings), we need to calculate 4% of the starting balance, then adjust the withdrawal for inflation annually, add in growth and show how this plays out over 30 years. We'll want inputs for starting balance, withdrawal rate, growth rate, inflation rate, age at retirement, and the number of years in retirement, so that we can fiddle with these numbers to see how they impact the final outcome:

Input	Description	Example value
Starting balance	Total retirement savings at the beginning	$1,000,000
Withdrawal rate	Initial withdrawal percentage	4%
Annual growth rate	Expected portfolio return	7%
Inflation rate	Annual cost-of-living increase	2.5%
Age at retirement	Starting age	65
Years in retirement	Duration of withdrawal period	30

In our Excel model, we'll use constant rates for both growth and inflation throughout the entire retirement period. This is a simplification that makes the model easier to build and understand. In reality, portfolio returns vary significantly from year to year (i.e. gains of 20% on year, others losses of 15% in another) and you would adjust withdrawals based on actual annual inflation rather than an assumed rate. The sequence of these returns matters a lot: poor market performance early in retirement is far more damaging than the same poor returns later on. This is called "sequence of returns risk," and it's why Bengen tested his 4% rule against historical market data, including worst-case scenarios like retiring in 1968 just before a major market decline and high inflation period. Our constant-rate model won't capture this real-world volatility, but it will demonstrate the mechanics of how the 4% rule works.

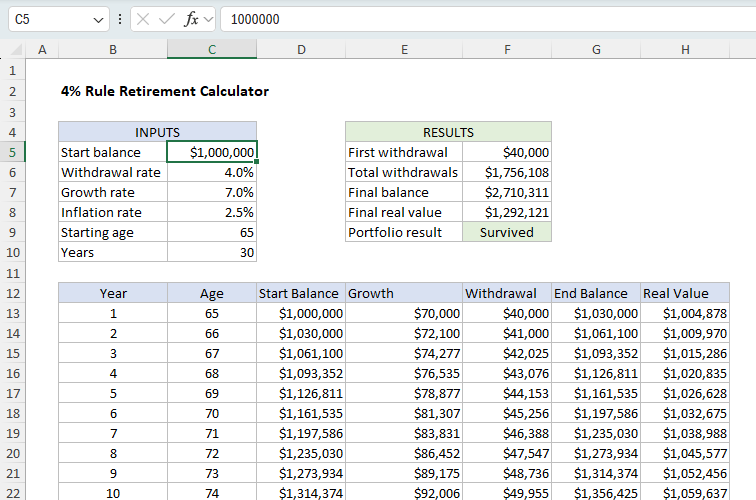
Using the inputs above, we need to generate a "withdrawal schedule" that shows how the portfolio changes over a period of 30 years. Once we have the schedule in place, we can calculate the total withdrawals and a final balance to see if the portfolio survived retirement. We also want to calculate a "real value" of the ending balance, adjusted for inflation. Finally, we want the withdrawal schedule to be dynamic, so that it expands or contracts as needed when the number of years in retirement changes. The screenshot below shows the basic idea. Note the key inputs are in the range C5:C10. These are the variables that control the outputs. The outputs are summarized in the range F5:F9. The withdrawal schedule begins in row 13 and covers 30 years.

The basic setup for the 4 percent rule model in Excel

The model in Excel

Of course, there are different ways to model a problem like this in Excel, especially since Excel now supports dynamic array formulas, which offer entirely new ways to approach multi-row calculations. The attached workbook explores three different ways to model the 4% retirement rule. All approaches use the same inputs and produce identical outputs, but they build the withdrawal schedule in progressively more advanced ways — from classic formulas to modern dynamic arrays.

Sheet1 - Traditional approach - Classic row-by-row formulas with relative and absolute references.
Sheet2 - Hybrid approach - One dynamic array formula per column.
Sheet3 - Single formula approach - One formula generates the entire table.

The workbook also has a fourth sheet with simple instructions on how to use the workbook.

The point of this exercise is not to convince you that one approach is better than the other. The point is to look at different ways to model a problem like this in Excel, and explore some of the pros and cons of each approach. Let's start with the traditional approach.

As shipped, all three worksheets have the same inputs and produce the same outputs. The only difference is the approach used to build the withdrawal schedule and the summary results in column F. On any sheet, you can modify the inputs in the range C5:C10 to see how the outputs change. The changes you make on one sheet will not affect the other sheets.

Traditional formula approach (Sheet1)

This worksheet uses a classic row-by-row setup — each row represents one year of retirement, and every column holds a key variable: Year, Age, Start Balance, Growth, Withdrawal, End Balance, and Real Value (inflation-adjusted balance). Formulas are copied down and use a mix of relative and absolute references so that each row refers correctly to the previous year’s results. It takes more than 200 formulas to build the entire withdrawal schedule for 30 years.

Modeling the 4% rule with traditional formulas

Here is how the formulas are set up:

Column	Description	Example formula (first data row)
B - Year	Sequence of years	`1` in row 13, then `B13+1`
C - Age	Age in each year	`=C9` in row 13, then `C13+1`
D - Start Balance	Beginning portfolio value	`=C5` in row 13, then `G13`
E - Growth	Portfolio growth	`=D13*$C$7`
F - Withdrawal	Inflation-adjusted withdrawal	`=C5C6` in row 13, then `=F13(1+$C$8)`
G - End Balance	End of year balance	`=D13+E13-F13`
H - Real Value	Inflation-adjusted end balance	`=PV($C$8,B13,0,-G13)`

The summary results in the range F5:F9 are generated with the following formulas:

Cell	Description	Formula
F5	First withdrawal	`=C5*C6`
F6	Total withdrawals	`=SUM(F13:F100)`
F7	Final balance	`=LOOKUP(2,1/(G13:G100<>""),G13:G100)`
F8	Total real value	`=LOOKUP(2,1/(H13:H100<>""),H13:H100)`
F9	Portfolio result	`=IF(F7>0,"Survived","Depleted")`

The LOOKUP function is used to find the last non-empty cell in the range G13:G100 and H13:H100. These ranges are oversized to allow the table to be extended if needed. For more details on this formula see Get value of last non-empty cell. The LOOKUP function works in all Excel versions. You could use the same trick to pull the last year in column B into C10 (Years) if you like, but I have left it as a static value to avoid confusion. For more information on the PV function, see PV function.

Note that a key feature of this approach is that formulas in row 1 of the schedule are often different from the formulas in the subsequent rows. These formulas must be carefully crafted to ensure that they reference the correct cells, which involves using a mix of relative and absolute references. It also means a user must be careful if changes are made to the withdrawal schedule. On the other hand, this approach is easy to understand and audit, and works in all Excel versions.

Pros and cons

Pros	Cons
Easy to understand and audit	Must copy or extend formulas manually
Works in all Excel versions	Fixed size, table is not dynamic
Great for teaching relative/absolute references	Prone to reference errors if rows are inserted or deleted

Hybrid formula approach (Sheet2)

This sheet uses dynamic array formulas to generate each full column of data automatically. Every column uses one formula that spills to the required number of rows, tied initially to the Years (C10) input. It takes 7 formulas to build the entire withdrawal schedule, one per column:

Modeling the 4% rule with dynamic array formulas and a hybrid approach

The formulas are set up like this:

Column	Description	Formula
B - Year	Sequence of years	`=SEQUENCE(C10)`
C - Age	Starting age + sequence	`=SEQUENCE(C10,1,C9)`
D - Start Balance	Prior year's end	`=VSTACK(C5,DROP(G13#,-1))`
E - Growth	Annual growth	`=D13#*C7`
F - Withdrawal	Inflation-adjusted withdrawal	`=FV(C8,B13#-1,0,-C5*C6)`
G - End Balance	Balance after growth and withdrawal	`=SCAN(C5,F13#,LAMBDA(bal,wd,bal*(1+C7)-wd))`
H - Real Value	Inflation-adjusted balance	`=PV(C8,B13#,0,-G13#)`

The summary results in the range F5:F9 are generated with the following formulas:

Cell	Description	Formula
F5	First withdrawal	`=C5*C6`
F6	Total withdrawals	`=SUM(F13#)`
F7	Final balance	`=TAKE(G13#,-1)`
F8	Total real value	`=TAKE(H13#,-1)`
F9	Portfolio result	`=IF(F7>0,"Survived","Depleted")`

This approach in Sheet2 is a great example of how formulas can be anchored to an existing spill range so that columns automatically expand or contract as needed. All the formulas in columns D through H are anchored to a spill range for years that begins in cell B13, so that they automatically adjust to the correct number of rows as needed. The spill range for years is generated with the SEQUENCE function like this:

=SEQUENCE(C10) // generate years 1 to 30

If the number of years in cell C10 is changed, the rows in the Year column will expand or contract as needed. Column C (Age) is also created with the SEQUENCE function, which is configured to generate a sequence of ages that spans the same number of years as the Year column, beginning at the starting age in cell C9, and increasing by 1 for each year.

=SEQUENCE(C10,1,C9) // generate ages 65 to 94

Column D (Start Balance) is generated with a clever combination of the DROP and VSTACK functions, like this:

=VSTACK(C5,DROP(G13#,-1))

DROP removes the last (unused) year-end balance from the spill range in column G (End Balance). VSTACK then inserts the starting balance in C5 at the top of the list and appends the year-end balance. It is a bit confusing that the start balance comes before the end balance, and yet the start balance depends on the end balance. But it makes sense if you think about it - the start balance is really the same as the end balance shifted down by one year. In other words, we need the end balance to know the starting balance in the next year.

Column E (Growth) is generated by multiplying the start balance by the growth rate:

=D13#*C7

Column F (Withdrawal) is generated by the FV function. The FV function calculates the future value of an investment based on an initial principal balance, a fixed annual interest rate, the number of compounding periods, and the periodic payment. In this case, we are using the FV function to calculate the future value of the initial withdrawal amount, adjusted for inflation, over the number of years in the withdrawal schedule. The formula looks like this:

=FV(C8,B13#-1,0,-C5*C6)

The rate is supplied as the inflation rate in C8 (2.5%), the number of periods is the number of years in the withdrawal schedule minus 1 B13#-1, the present value is the starting balance multiplied by the withdrawal rate -C5*C6, and the payment is 0 since there are no periodic payments.

We use the FV function here to calculate an inflation-adjusted withdrawal, but we could use the equivalent long-hand formula: =C5*C6*(1+C8)^(B13#-1). Both formulas will return the same result.

Column G (End Balance) is generated by the SCAN function. The SCAN function applies a LAMBDA function to a series of values and accumulates the results. In this case, we are using the SCAN function to calculate the year-end balances by applying the LAMBDA function to the starting balance and the withdrawal. The formula looks like this:

=SCAN(C5,F13#,LAMBDA(bal,wd,bal*(1+C7)-wd))

The starting balance is supplied as the starting value in C5, the series of values is the series of withdrawals in F13#, and the LAMBDA function is LAMBDA(bal,wd,bal*(1+C7)-wd). The LAMBDA function is applied to the starting value and the first value in the series, and the result is returned. The result is then used as the starting value for the next iteration of the LAMBDA function. This process is repeated for each value in the series. With 30 years in C10, the result is a series of 30 year-end balances.

Column H (Real Value) is generated by the PV function. The PV function calculates the present value of an investment based on a future value, a fixed annual interest rate, the number of compounding periods, and the periodic payment. In this case, we are using the PV function to calculate the present value of the year-end balances, adjusted for inflation. The formula looks like this:

=PV(C8,B13#,0,-G13#)

The rate is supplied as the inflation rate in C8 (2.5%), the number of periods is the number of years in the withdrawal schedule B13#, the future value is the year-end balances in G13#, and the payment is 0 since there are no periodic payments.

We use the PV function here to calculate an inflation-adjusted end balance, but we could use the equivalent long-hand formula: =G13#/(1+$C$8)^(B13#). Both formulas will return the same result.

As mentioned above, because these formulas are tied to the spill ranges, beginning with the spill range in column B (Year), all columns will resize as needed if the number of years in retirement C10 is changed.

Excel's PV and FV functions use a cash flow convention where you negate values that represent outflows. This is why the present value is negative in the FV function and the future value is positive in the PV function. The negative sign ensures that we get a positive result.

Pros and cons

Pros	Cons
Fully dynamic — table resizes automatically	Requires Excel 365
One formula per column, no locked references	Depends on anchoring to spill ranges
Clean, scalable, and easy to read	New functions like SCAN and VSTACK may be unfamiliar
Fewer formulas to manage	More abstract than row-by-row approach

Single formula approach (Sheet3)

In this sheet, the entire withdrawal schedule is generated by a single dynamic array formula that combines LET, SEQUENCE, FV, SCAN, VSTACK, and HSTACK. Each variable is defined and reused inside a single expression, which spills into a complete table. It takes 9 formulas to build the entire withdrawal schedule:

Modeling the 4% rule with a single dynamic array formula

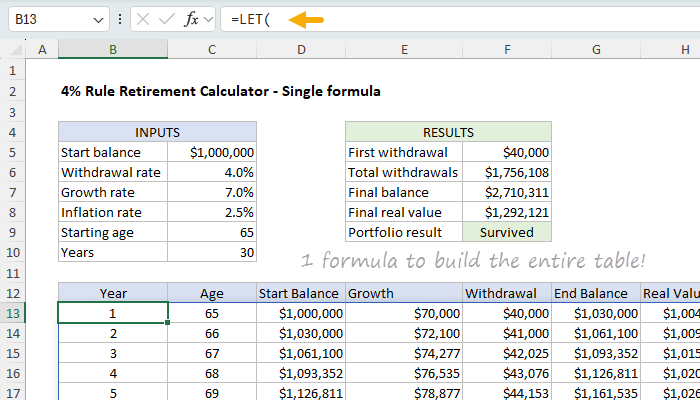
The formula in B13 looks like this:

=LET(
  start,C5, wr,C6, gr,C7, ir,C8, age,C9, n,C10,
  yrs,SEQUENCE(n),
  ages,SEQUENCE(n,1,age),
  wds,FV(ir,yrs-1,0,-start*wr),
  ends,SCAN(start, wds, LAMBDA(bal,wd, bal*(1+gr)-wd)),
  starts,VSTACK(start,DROP(ends,-1)),
  growth,starts*gr,
  real,PV(ir,yrs,0,-ends),
  HSTACK(yrs,ages,starts,growth,wds,ends,real)
)

This formula uses the LET function to define a series of variables that are used to generate the withdrawal schedule:

Variable	Description
start	Starting portfolio balance from C5 ($1,000,000)
wr	Withdrawal rate from C6 (4%)
gr	Annual growth rate from C7 (7%)
ir	Inflation rate from C8 (2.5%)
age	Starting age from C9 (65)
n	Number of years from C10 (30)
yrs	Sequence of years 1 to n
ages	Sequence of ages starting at age
wds	Annual withdrawals, adjusted for inflation via FV function
ends	Year-end balances generated by SCAN
starts	Start balances built from prior year's end
growth	Annual growth amounts from start balance * growth rate
real	Inflation-adjusted end balances via PV function

The summary results in the range F5:F9 are generated with the following formulas:

Cell	Description	Formula
F5	First withdrawal	`=C5*C6`
F6	Total withdrawals	`=SUM(CHOOSECOLS(B13#,5))`
F7	Final balance	`=TAKE(CHOOSECOLS(B13#,6),-1)`
F8	Total real value	`=TAKE(CHOOSECOLS(B13#,7),-1)`
F9	Portfolio result	`=IF(F7>0,"Survived","Depleted")`

This is clearly the most complex formula of the three approaches, but it is also the most compact and efficient. One nice feature of building the formula this way is that once the variables are defined, they can be used directly in other parts of the formula instead of cell references, making the formula easier to read and understand. Briefly, the formula works like this:

Define the starting balance (start), withdrawal rate (wr), growth rate (gr), inflation rate (ir), starting age (age), and number of years (n). start,C5, wr,C6, gr,C7, ir,C8, age,C9, n,C10
Generate a sequence of years (yrs) from 1 to n. yrs,SEQUENCE(n)
Generate a sequence of ages (ages) starting at the starting age. ages,SEQUENCE(n,1,age)
Generate a series of annual withdrawals (wds), adjusted for inflation via the FV function. wds,FV(ir,yrs-1,0,-start*wr)
Generate a series of year-end balances (ends) by applying the SCAN function to the starting balance and the series of annual withdrawals. ends,SCAN(start, wds, LAMBDA(bal,wd, bal*(1+gr)-wd))
Generate a series of start balances (starts) by building from the prior year's end. starts,VSTACK(start,DROP(ends,-1))
Generate a series of annual growth amounts (growth) by multiplying the start balance by the growth rate. growth,starts*gr
Generate a series of inflation-adjusted end balances (real) by applying the PV function to the year-end balances. real,PV(ir,yrs,0,-ends)
Combine all the series into a single table using the HSTACK function. HSTACK(yrs,ages,starts,growth,wds,ends,real)

For details on the functions used in the formula, see the Functions used in the workbook section below.

Pros and cons

Pros	Cons
One formula builds the entire table	Advanced Excel skills required
Fully dynamic, no fixed ranges	Requires Excel 365
Compact and efficient	Steeper learning curve
Single source of truth	Harder to audit cell-by-cell

Summary and conclusion

All three worksheets produce the same result: a year-by-year simulation of the 4% retirement rule. The difference lies in how the withdrawal schedule is built.

Traditional (Sheet1) builds the table step-by-step using relative and absolute references.
Hybrid (Sheet2) constructs each column with a single dynamic array formula.
Single (Sheet3) uses one dynamic array formula to generate the entire table.

Each approach is valid — your choice depends on your priorities for transparency and flexibility, and your comfort level with modern Excel features. Which approach do you like best?

Approach	Strengths	Limitations	Best use case
Traditional	Simple, visual, easy to follow	Manual setup, not dynamic	Teaching, compatibility with older Excel
Hybrid	Dynamic arrays, clear logic, no locked references	Requires Excel 365	Modern Excel modeling, learning SCAN and VSTACK
Single	Fully dynamic, one formula, easy to reuse	Harder to audit visually	Reusable templates, LAMBDA functions, advanced modeling

Functions used in the workbook

The models in the attached workbook use many Excel functions, some of which you might not be familiar with. Below is a list of the functions used, with links to pages with more details and examples. If you are new to dynamic array formulas, you might also want to check out this article: Dynamic array formulas in Excel.

Function	Description
CHOOSECOLS	Extracts specific columns from an array
DROP	Removes rows or columns from the beginning or end of an array
FV	Calculates the future value of an investment
HSTACK	Combines arrays horizontally (side by side)
IF	Returns one value if a condition is true, another if false
LAMBDA	Creates custom functions using Excel's formula language
LET	Assigns names to calculation results for use in formulas
PV	Calculates the present value of an investment
SCAN	Applies a function to each element in an array and returns intermediate results
SEQUENCE	Generates a sequence of numbers
SUM	Adds numbers in a range or array
TAKE	Returns a specified number of rows or columns from an array
VSTACK	Combines arrays vertically (stacked on top of each other)

Instructions

As shipped, all three worksheets have the same inputs and produce the same outputs. The only difference is the approach used to build the withdrawal schedule. On any sheet, you can modify the inputs in the range C5:C10 to see how the outputs change. The changes you make on one sheet will not affect the other sheets. For example, if you change the starting balance in C5 on Sheet1 from $1,000,000 to $1,500,000, the starting balance in the other two sheets will not change.

Click through the 3 worksheets to see how the withdrawal schedule is built.
Modify the input cells in column C to test different scenarios.
Watch how the projection table updates automatically.
Pay attention to the Final Balance in E7 — does it go negative?
Compare Real Value to see inflation’s impact on purchasing power.

Notes

While my Excel model uses constant growth and inflation rates for simplicity, Bengen's original research was far more rigorous. He used actual historical data from 1926 onward, testing over 50 different 30-year retirement periods with the real year-by-year stock returns, bond returns, and inflation rates. This included the Great Depression, the 1970s stagflation, bull markets, bear markets, and everything in between. Bengen tested multiple portfolio allocations ranging from 0% to 100% stocks, focusing primarily on 50/50 and 75/25 stock-to-bond splits. The 4% withdrawal rate emerged because it was the maximum rate that survived even the worst historical scenario (retiring late in 1968). The beauty of his approach was testing against actual market sequences, not constant averages.