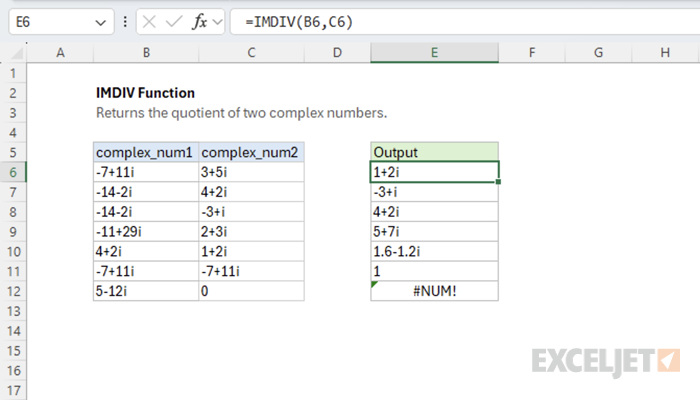
Purpose
Return value
Syntax
=IMDIV(complex_num1,complex_num2)- complex_num1 - The first complex number.
- complex_num2 - The second complex number.
Using the IMDIV function
The Excel IMDIV function returns the quotient of two complex numbers. For example, given "-7+11i" and "3+5i" as input, the function returns the quotient "1+2i", which is the result of dividing the first number by the second.
=IMDIV(COMPLEX(-7,11),COMPLEX(3,5)) // returns 1+2i
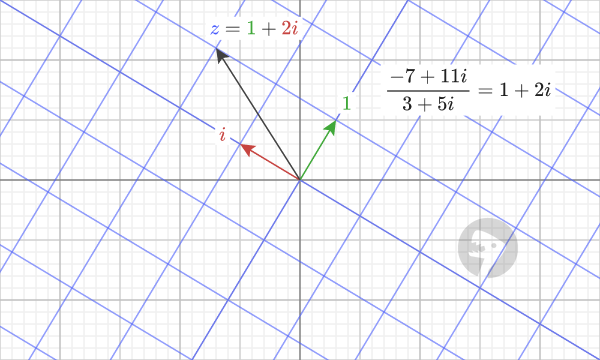
The quotient of two complex numbers can be visualized by uniformly stretching and rotating the coordinate system so that "1" goes to the complex number, which is the divisor. In this case, the transformed coordinate system (shown in blue) is stretched and rotated so that "1" (shown as the green arrow) goes to the point "3+5i". The quotient represents how to get to the first complex number, "-7 +11i", in terms of the transformed coordinates.
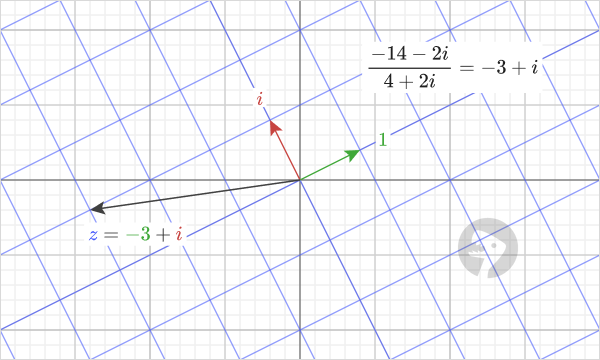
Here's another example: the result of dividing "-14-2i" by "4+2i" is equal to "-3+i".
=IMDIV(COMPLEX(-14,-2),COMPLEX(4,2)) // returns -3+i
If we uniformly stretch and rotate the coordinate system so that the green arrow, "1", goes to the point "4+2i", we can see that to get to the point "-14-2i" we travel "-3+i" units in the transformed coordinate system.
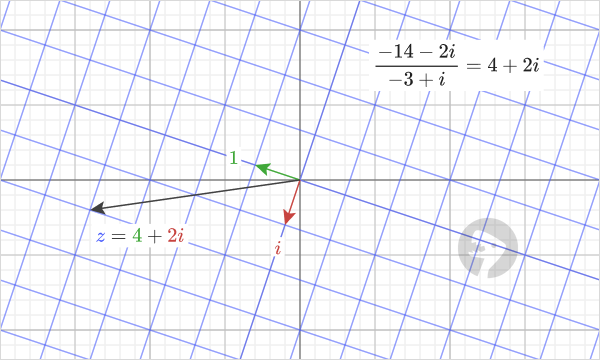
We can visualize the example that corresponds to this one by switching the divisor with the quotient. In other words, the result of dividing "-14-2i" by "-3+i" is equal to "4+2i".
=IMDIV(COMPLEX(-14,-2),COMPLEX(-3,1)) // returns 4+2i
When we uniformly stretch and rotate the coordinate system so that the green arrow, "1", goes to the point "-3+i", now we travel "4+2i" units in the transformed coordinate system to get to the point "-14-2i".
Explanation
When dividing complex numbers, it's not obvious how to calculate the result by hand.

Compare this to complex multiplication, where we can use algebra to multiply two complex numbers.

The key to dividing two complex numbers is to convert the problem into one we know how to solve. This is done by using the fact that multiplying a complex number by its conjugate equals a real number.

This changes the denominator into a real number, which we know how to divide by. This is how we can manually calculate the quotient of two complex numbers in Excel.
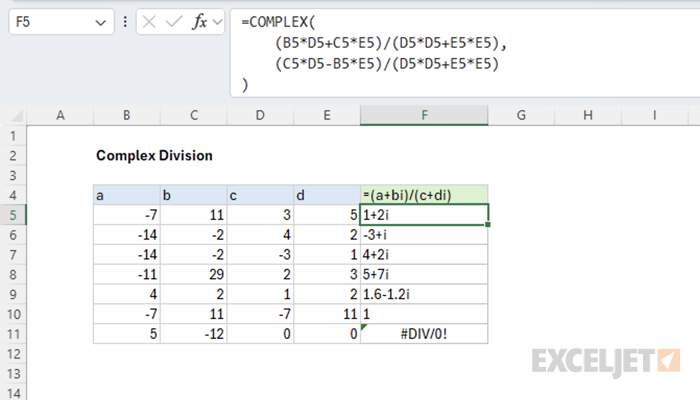
There is a slight difference between this formula and the IMDIV function because IMDIV returns a #NUM! error instead of #DIV/0! when dividing by zero.
Images courtesy of wumbo.net.