GAMMALN Function

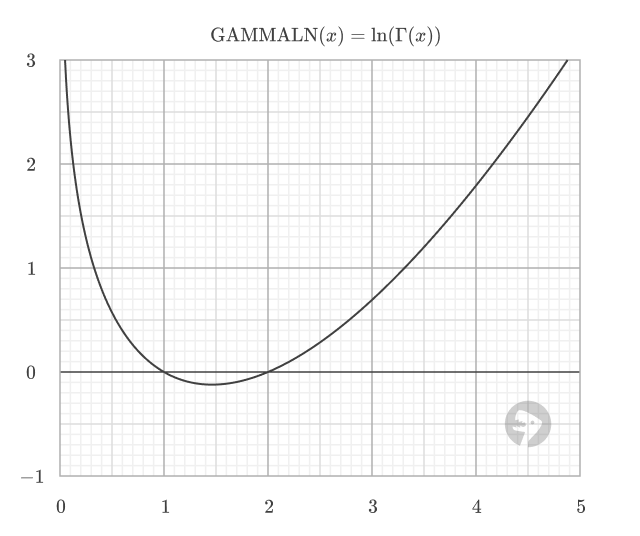
The GAMMALN function returns the natural logarithm of the gamma function, ln(Γ(n)), for a given number. This is especially useful in statistical calculations, such as those involving probability distributions, where the gamma function appears in the denominator and direct computation could result in very large or very small numbers. For positive integers n, GAMMALN(n) is equivalent to LN((n-1)!).

For example, the following formula calculates the natural logarithm of the gamma value for 5:

=GAMMALN(5) // returns 3.17805383

Key features

• Returns the natural logarithm of the gamma function for decimal numbers
• For positive integers n, GAMMALN(n) equals LN((n-1)!)
• Accepts positive decimal numbers as input
• Returns #NUM! error for zero and negative numbers

Table of contents

• Key features
• Example #1 - Basic calculations
• Example #2 - Relationship to gamma and factorials
• Example #3 - Error conditions
• Formula definition

GAMMALN is still available for compatibility with earlier versions of Excel, but has been replaced by GAMMALN.PRECISE, which provides improved accuracy. Microsoft recommends using GAMMALN.PRECISE for new work.

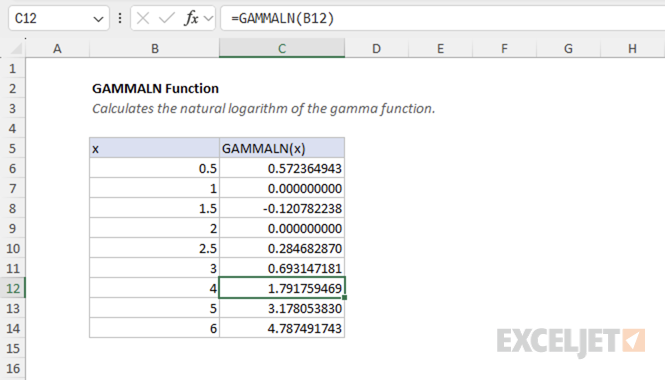
Example #1 - Basic calculations

The GAMMALN function takes a single argument as input like this:

=GAMMALN(x)

The argument x is the value for which you want to calculate the natural logarithm of the gamma function. Here are some basic examples showing both integer and non-integer inputs:

=GAMMALN(0.5) // returns 0.57236494...
=GAMMALN(2.0) // returns 0
=GAMMALN(2.5) // returns 0.28468287...
=GAMMALN(4.0) // returns 1.79175947...

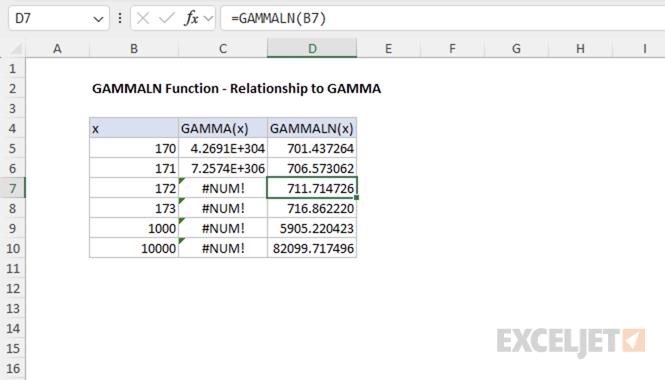
Example #2 - Relationship to gamma and factorials

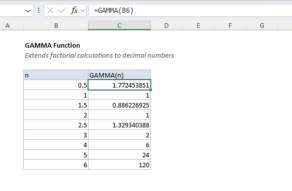
In general, the GAMMALN function is equivalent to the natural logarithm of the GAMMA function:

=GAMMALN(x) // returns LN(GAMMA(x))

This relationship makes the GAMMALN function useful for calculations involving large factorials, as it avoids direct computation of large numbers. For example, attempting to compute a large factorial directly with the GAMMA function can result in an error due to overflow:

=GAMMA(172) // returns #NUM! error

In contrast, using GAMMALN allows you to work with the logarithm of the gamma function, which avoids this problem and provides a valid result even for large inputs.

Example #3 - Error conditions

The GAMMALN function returns #NUM! for zero and negative numbers, and #VALUE! for non-numeric inputs.

=GAMMALN(0) // returns #NUM! error
=GAMMALN(-1) // returns #NUM! error
=GAMMALN(-2.5) // returns #NUM! error
=GAMMALN("text") // returns #VALUE! error

Formula definition

The GAMMALN function is defined as the natural logarithm of the gamma function. Shown below is the plot of the GAMMALN function, where Γ(x) is the gamma function.