GAMMA Function

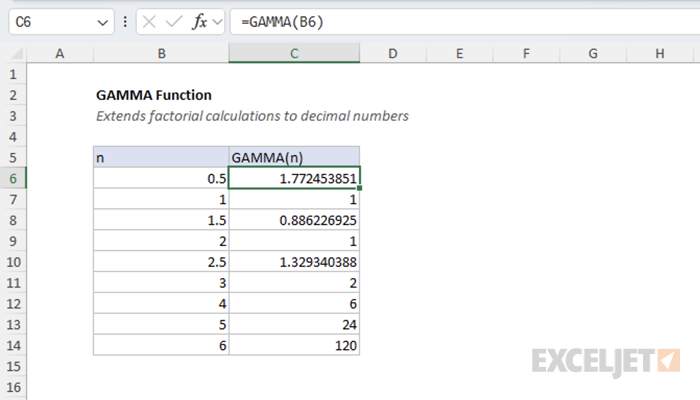
The GAMMA function returns the gamma function value Γ(n) for a given number. The key relationship to understand is that Γ(n) = (n - 1)!, which means Excel's GAMMA function essentially computes factorials shifted by one position. For example, GAMMA(5) returns 24, which is equivalent to 4! (4 factorial). Importantly, the gamma function extends this factorial concept to non-integer values, defining calculations like GAMMA(2.5) that would be undefined with traditional factorials.

The GAMMA function is used for statistical calculations, probability distributions, and advanced mathematical modeling.

Key features

• Returns the gamma function value for decimal numbers
• For positive integers n, GAMMA(n) equals (n-1)!
• Accepts positive decimal numbers as input
• Returns #NUM! error for zero and negative integers

Table of contents

• Example #1 - Basic calculations
• Example #2 - Relationship to factorials
• Example #4 - Error conditions
• Mathematical Definition
• Notes

Example #1 - Basic calculations

The GAMMA function takes a single argument in this syntax:

=GAMMA(number)

The argument number is the value for which you want to calculate the gamma function. Here are some basic examples showing both integer and non-integer inputs:

=GAMMA(0.5) // returns 1.7724538509... (√π)
=GAMMA(2) // returns 1
=GAMMA(2.5) // returns 1.3293403881...
=GAMMA(5) // returns 24

Example #2 - Relationship to factorials

The example below demonstrates the relationship between the GAMMA function and factorials. For any positive integer n, GAMMA(n) equals (n-1)!.

=GAMMA(n) // returns (n-1)!

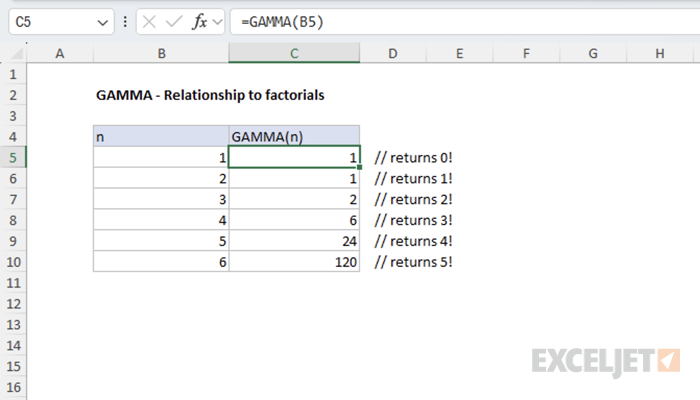
This relationship makes the GAMMA function particularly useful when you need factorial-like calculations for non-integer values or in statistical formulas.

Example #3 - Error conditions

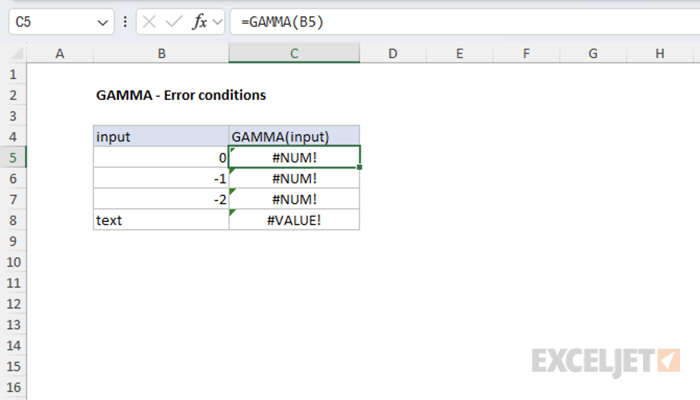
The GAMMA function returns #NUM! for zero and negative integers, and #VALUE! for non-numeric inputs.

=GAMMA(0) // returns #NUM! error
=GAMMA(-1) // returns #NUM! error
=GAMMA(-2) // returns #NUM! error
=GAMMA("text") // returns #VALUE! error

Mathematical Definition

The gamma function is formally defined as an integral that extends the concept of factorials to real and complex numbers. The mathematical definition is:

While the gamma function is mathematically defined for complex numbers, Excel's GAMMA function implementation only accepts positive real number inputs.

Notes

• Decimal and positive values are accepted and return valid results
• For positive integers n, GAMMA(n) = (n-1)!
• The function returns #NUM! error for zero and negative integers
• The GAMMA function is used for advanced statistical and mathematical calculations