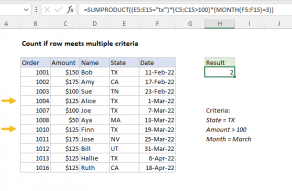
Explanation
Working from the inside out, the logical criteria used in this formula is:
(data)<70
where data is the named range C5:I14. This generates a TRUE / FALSE result for every value in data, and the double negative coerces the TRUE FALSE values to 1 and 0 to yield an array like this:
{0,0,0,1,0,1,0;0,0,0,0,0,0,0;0,0,0,0,0,0,0;0,1,1,0,0,1,0;0,0,0,0,0,0,0;0,0,0,0,0,0,0;0,0,0,0,0,0,0;0,1,0,0,0,0,0;0,0,0,0,0,0,0;0,0,0,0,0,0,0}
Like the original data, this array is 10 rows by 7 columns (10 x 7) and goes into the MMULT function as array1. The next argument, array2 is created with:
TRANSPOSE(COLUMN(data)^0))
Here, the COLUMN function is used as a way to generate a numeric array of the right size, since matrix multiplication requires the column count in array1 (7) to equal the row count in array2.
The COLUMN function returns the 7-column array {3,4,5,6,7,8,9}. By raising this array to a power of zero, we end up with a 7 x 1 array like {1,1,1,1,1,1,1}, which TRANSPOSE changes to a 1 x 7 array like {1;1;1;1;1;1;1}.
MMULT then runs and returns a 10 x 1 array result {2;0;0;3;0;0;0;1;0;0}, which is processed with the logical expression >=2, resulting in an array of TRUE FALSE values:
{TRUE;FALSE;FALSE;TRUE;FALSE;FALSE;FALSE;FALSE;FALSE;FALSE}
We again coerce TRUE FALSE to 1 and 0 with a double negative to get a final array inside SUM:
=SUM({1;0;0;1;0;0;0;0;0;0})
Which correctly returns 2, the number of names with at least 2 scores below 70.