IMLN Function

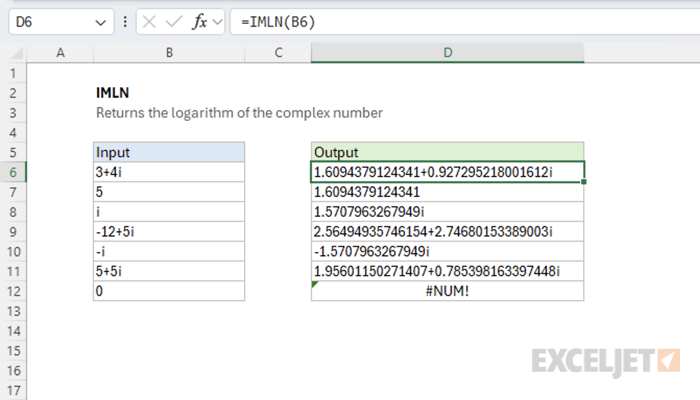
The Excel IMLN function returns the natural logarithm of a complex number. For example, given the complex number "3+4i" as input, the function returns the logarithm of the complex number.

=IMLN(COMPLEX(3,4)) // returns 1.6094379124341 + 0.927295218001612i

The real part of the output is equal to the natural logarithm of the distance from the origin to the point "3+4i" in the complex plane.

=LN(IMABS(COMPLEX(3,4))) // returns 1.609437912

The imaginary part of the output is equal to the angle in radians of the complex number relative to the positive real axis.

=IMARGUMENT(COMPLEX(3,4)) // returns 0.927295218

Explanation

Given a complex number z, the complex logarithm is defined as:

• The radius r represents the distance from the origin to the point z in the complex plane.
• The angle θ represents the angle in radians of the complex number z relative to the positive real axis.

In Excel, the complex logarithm is equal to the following formula where cell B6 contains a complex number:

=COMPLEX(LN(IMABS(B6)),IMARGUMENT(B6))

Visualizing the Output

The 3D graph below visualizes the real part of the function's output. The horizontal XY-plane represents the input in the complex plane, and the vertical axis represents the function's real output.

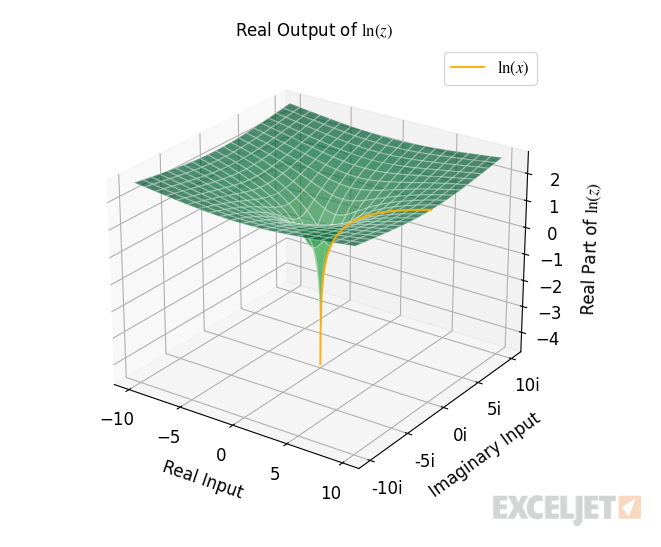
Geometrically, the real part of the function's output equals the natural logarithm of the distance from the origin to the point in the complex plane.

=IMREAL(IMLN(COMPLEX(3,4))) // returns 1.609437912434100

The 3D graph below visualizes the imaginary part of the function's output. The horizontal XY-plane represents the input in the complex plane, and the vertical axis represents the function's imaginary output.

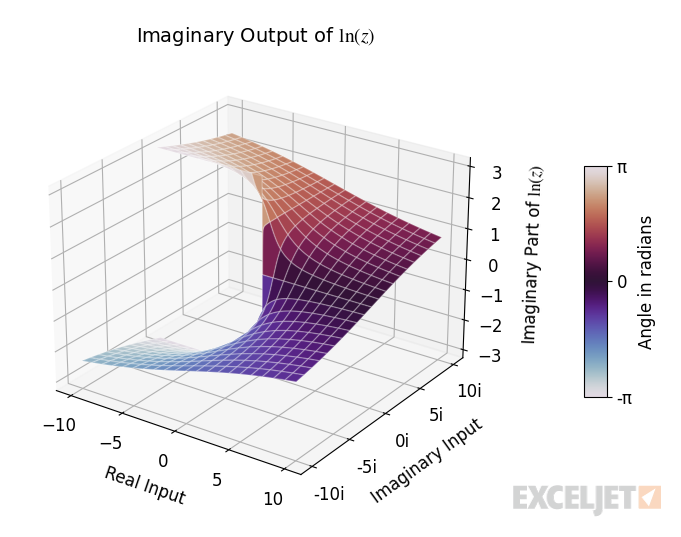
Geometrically, the imaginary part equals the angle in radians of the complex number output by the function.

=IMAGINARY(IMLN(COMPLEX(3,4))) // returns 0.927295218

Relationship to the Exponential

In the context of complex numbers, the logarithm and exponential function have a slightly different relationship than they do in the context of real numbers, where they are inverses of each other. Their relationship is the same when you pass the output of the logarithm to the exponential; the result is the original input.

=IMEXP(IMLN(COMPLEX(x,y))) // always returns x+yi

However, their relationship is different when you pass the output of the exponential to the logarithm; the result isn't necessarily the original input.

=IMLN(IMEXP(COMPLEX(x,y))) // doesn't necessarily return x+yi

The difference is because of the exponential function's periodic nature. For example, consider a complex number written in terms of its radius and angle (polar form).

The angle that describes the number can take on infinitely many values. Because if you add 2π to any angle, you get an equivalent complex number. This is why the complex logarithm is multivalued and could be expressed like this, where k is some integer.

To make the complex logarithm single-valued, the angle is restricted to a particular range from -π to π. This is called a branch cut, and it removes the ambiguity of the multiple angles that can describe the same complex number. The consequence of the branch cut is the function sometimes returns an equivalent angle mapped to the range from -π to π, which includes π and excludes -π.

For example, given the expression IMEXP("2 + 3π i") as input, the complex logarithm returns "2+π i".

=IMLN(IMEXP(COMPLEX(2,3*PI()))) // returns 2+πi

Branch Cut

The behavior of the complex logarithm for its branch cut can be demonstrated with the complex number "-1-1i". If you rotate the positive direction to the point in the complex plane, the rotation is equal to 5/4 π radians. Equivalently, if you rotate in the negative direction to the point in the complex plane, the rotation is equal to -3/4 π radians.

In this case, the complex logarithm returns the branch cut from -π to π, so the returned angle is -3/4 π.

=IMAGINARY(IMLN(COMPLEX(-1,-1))) // returns -3/4π

Of course, many more angles correspond to the point "-1-1i". Any angle outside the range -π to π gets mapped to the branch cut.

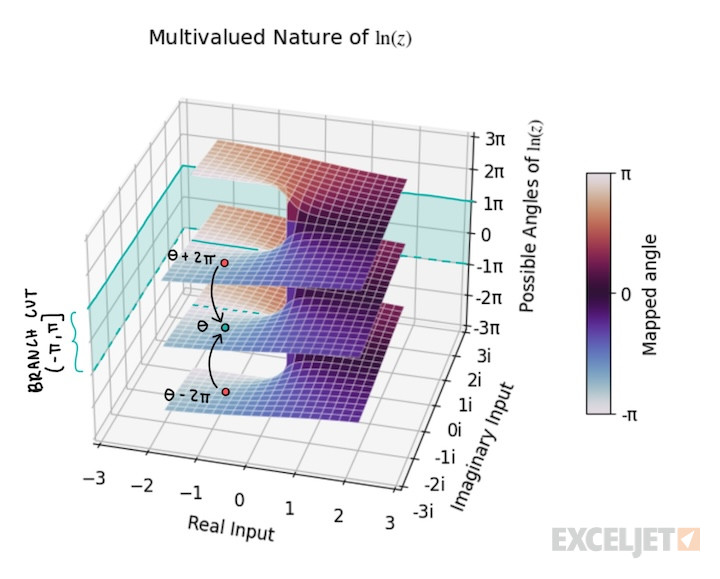
The range of the branch cut is (-π, π], which excludes -π and includes π. This means that for points that lie on the negative real axis, where the branch cut occurs, the returned angle is π.

=IMAGINARY(IMLN(COMPLEX(-1,0))) // returns π

The discontinuous jump of the branch cut is visualized by the 3D plot below.

Images courtesy of wumbo.net.

Notes

• The function returns a #NUM! error when given zero input