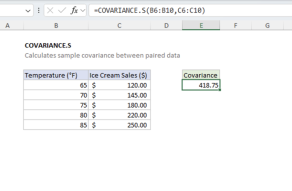
Purpose
Return value
Syntax
=CORREL(array1,array2)- array1 - The first set of data values.
- array2 - The second set of data values.
Using the CORREL function
The CORREL function calculates the Pearson correlation coefficient between two data sets. It measures both the strength and direction of the linear relationship between variables, providing a standardized measure that ranges from -1 to 1.
Key features
- Returns values between -1 and 1 (inclusive)
- Positive values close to 1 indicate positive correlation
- Negative values close to -1 indicate negative correlation
- Values close to zero indicate weak correlation
- Unit-independent and standardized measure
- Both arrays must have the same number of data points
- Works with numbers only - text and logical values are ignored
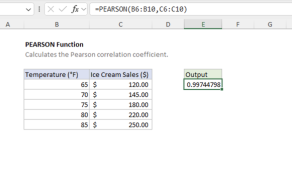
Note: Excel also provides PEARSON function which is identical to CORREL. Both calculate the Pearson product-moment correlation coefficient.
Table of contents
- Example #1 - Strong Positive Correlation
- Example #2 - Strong Negative Correlation
- Example #3 - Weak Correlation
- When to use CORREL
- Formula Definition
- Notes
Example #1 - Strong Positive Correlation
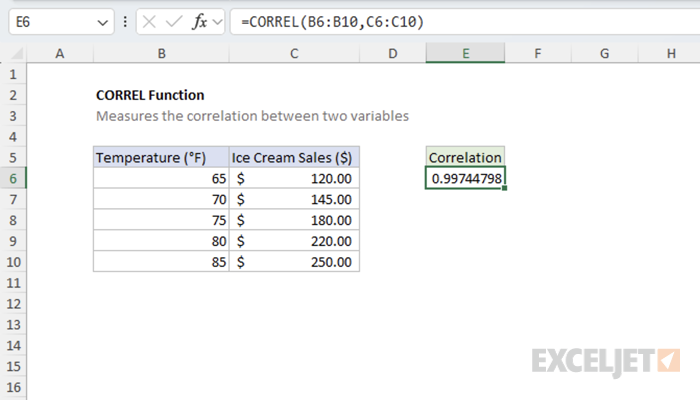
In this example, we'll examine the relationship between temperature (°F) and ice cream sales ($). As temperature increases, ice cream sales tend to increase as well, demonstrating a strong positive correlation.
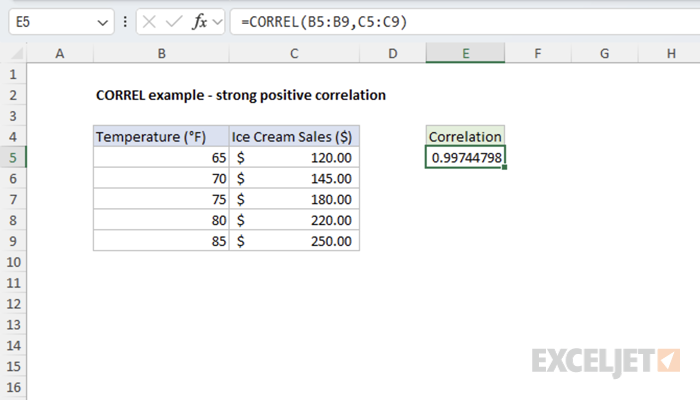
=CORREL(B5:B9,C5:C9) // returns 0.997447985
The result indicates a strong positive correlation between temperature and ice cream sales.
Example #2 - Strong Negative Correlation
Here we examine the relationship between a car's mileage (miles) and its resale value. As mileage increases, the car's value decreases proportionally, showing a strong negative correlation.
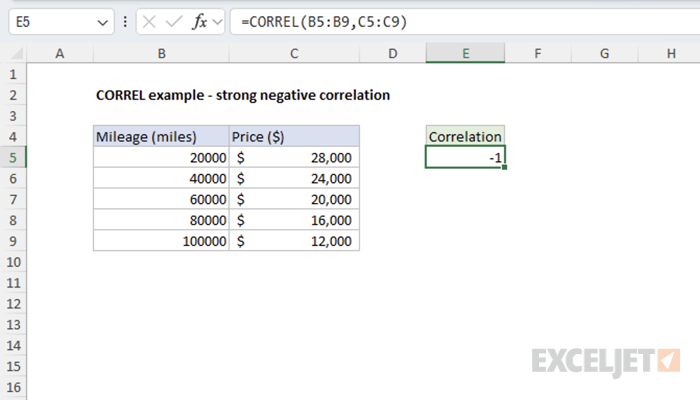
=CORREL(B5:B9,C5:C9) // returns -1
The result confirms a strong negative correlation between car mileage and its market value.
Example #3 - Weak Correlation
This example illustrates two variables with a weak relationship: daily temperature and coffee sales. While there might be some relationship, it's not very strong.
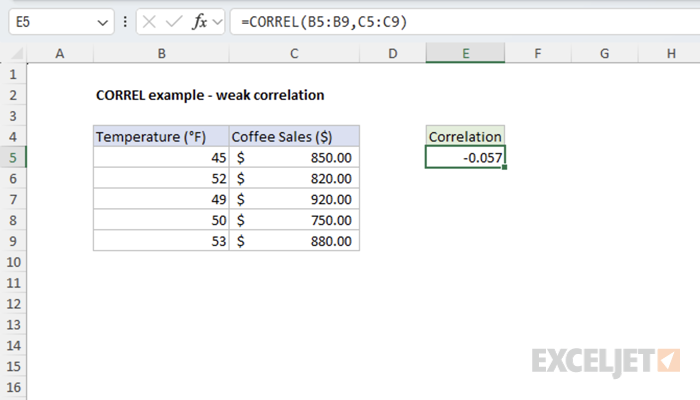
=CORREL(B5:B9,C5:C9) // returns -0.057
The result close to zero indicates a weak negative correlation between temperature and coffee sales.
When to use CORREL
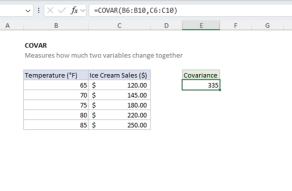
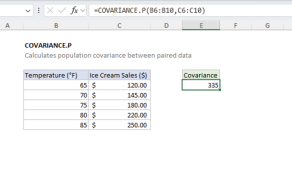
Use CORREL when you need to quantify the linear relationship between two sets of numerical data in Excel. Choose CORREL over COVARIANCE.P or COVARIANCE.S (covariance functions) when you want a standardized measure that's easy to interpret regardless of the units involved. Use the covariance functions when you care about the magnitude of change in addition to the direction and strength of the relationship between variables.
Key advantages
- Standardized scale (-1 to +1) makes interpretation easier
- Unit-independent - can compare relationships across different measurement scales
- Provides both direction and strength of relationship
- Widely recognized and understood statistical measure
Formula definition

Notes
- Both arrays must contain the same number of values
- Empty cells, text, and logical values are ignored
- Returns #DIV/0! error if either array has zero variance (all values are identical)
- Returns #N/A error if arrays have different lengths
- Only measures linear relationships - may miss non-linear associations