COVARIANCE.S Function

The COVARIANCE.S function calculates the sample covariance between two data sets. It measures the degree to which two variables vary together, providing insight into their linear relationship. The return value from the function is a single number that can be positive, negative, or zero, depending on the relationship between the variables. Unlike correlation, covariance is not standardized and depends on the units of measurement.

Key features

• Calculates sample covariance (divides by N-1, not N)
• Both arrays must have the same number of data points
• Returns positive values when variables move together
• Returns negative values when variables move in opposite directions
• Returns values close to zero when variables are independent
• Works with numbers only - text and logical values are ignored

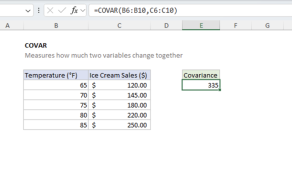
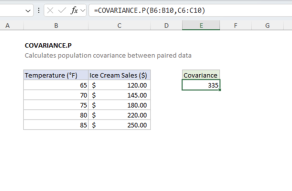
Note: Excel also provides COVARIANCE.P (population) function for population covariance. Use COVARIANCE.S when working with a sample from a larger population, and COVARIANCE.P when working with the entire population.

Table of contents

• Example #1 - Positive Sample Covariance
• Example #2 - Negative Sample Covariance
• Example #3 - Zero Sample Covariance
• When to use COVARIANCE.S
• COVARIANCE.S vs COVARIANCE.P

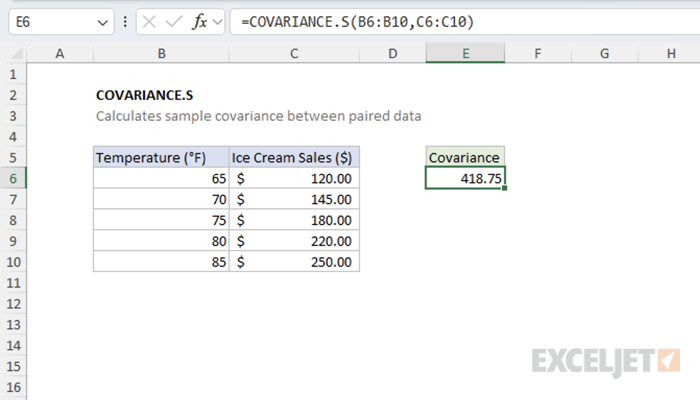
Example #1 - Positive Sample Covariance

In this example, we'll examine the relationship between temperature (°F) and ice cream sales ($) from a sample of 5 days. As temperature increases, ice cream sales tend to increase as well, demonstrating positive covariance.

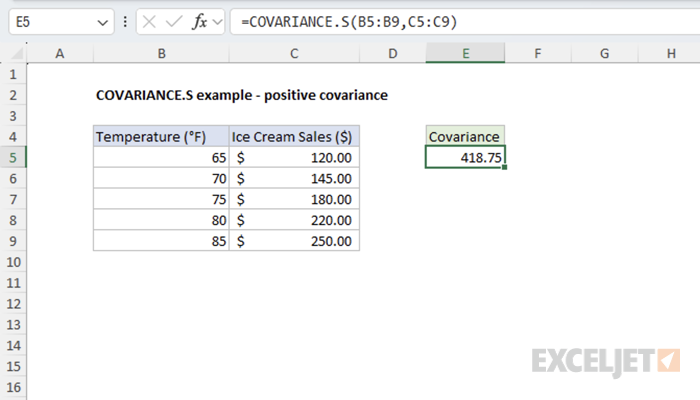
=COVARIANCE.S(B5:B9,C5:C9) // returns positive sample covariance

The positive result indicates that temperature and ice cream sales have a positive relationship in this sample. As one increases, the other increases too.

Example #2 - Negative Sample Covariance

Here we examine the relationship between a car's mileage and its resale price from a sample of vehicles. As mileage increases, the car's value typically decreases, showing negative covariance.

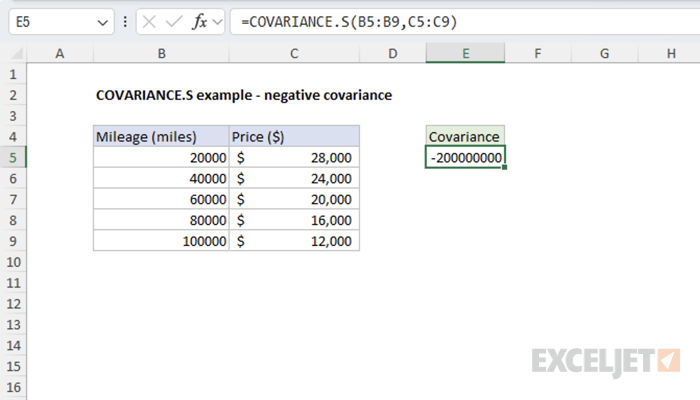
=COVARIANCE.S(B5:B9,C5:C9) // returns negative sample covariance

The negative result confirms that mileage and car price have an inverse relationship in this sample. As one increases, the other decreases.

Example #3 - Zero Sample Covariance

This example illustrates two variables with no linear relationship: daily temperature and the result of a dice roll from a 10-day sample. These variables are completely independent of each other.

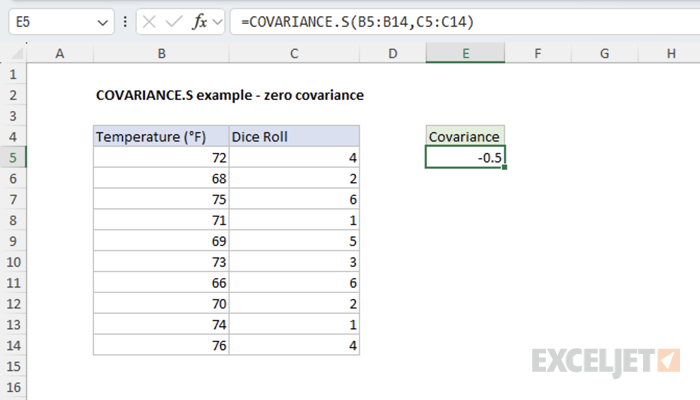
=COVARIANCE.S(B5:B14,C5:C14) // returns value close to zero

The result close to zero indicates no meaningful relationship between temperature and dice roll outcomes in this sample.

When to use COVARIANCE.S

Use the COVARIANCE.S function when you need to analyze paired sample data to understand whether a relationship exists between the two variables in the broader population. A positive covariance indicates that the two variables tend to move in the same direction. A negative covariance suggests that the variables move in opposite directions. If the result is near zero, it implies there is little to no linear relationship between the two data sets.

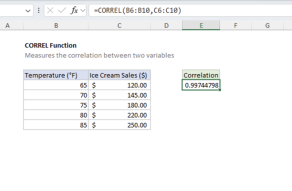
The magnitude of the covariance depends on the units of measurement. As a result, it can be challenging to determine the strength of a relationship between two variables from covariance alone. When you care about the magnitude of change between variables in a sample, COVARIANCE.S might be the appropriate function for your use case. Otherwise, for a standardized comparison, use the correlation function.

COVARIANCE.S vs COVARIANCE.P

The key difference between COVARIANCE.S and COVARIANCE.P lies in how they calculate the covariance:

• COVARIANCE.S (Sample Covariance): Divides by N-1, where N is the number of data points. Use this when your data represents a sample from a larger population.
• COVARIANCE.P (Population Covariance): Divides by N. Use this when your data represents the entire population of interest.

For most practical applications where you're working with sample data, COVARIANCE.S is the appropriate choice as it provides an unbiased estimate of the population covariance.

Formula definition of COVARIANCE.S

Notes

• Empty cells, text, and logical values are ignored
• Returns #DIV/0! error if arrays are empty after ignoring non-numeric values
• Returns #N/A error if arrays have different lengths
• Requires at least 2 data points to calculate (since it divides by N-1)
• For population covariance (divides by N), use COVARIANCE.P function