Repeat sequence of numbers

In this example, the goal is to repeat a sequence of numbers. This is a useful way to create repeating sequences of numbers by itself. In addition, this formula is a building block to the more general formula here, which can repeat ranges and arbitrary values that are not sequential numbers.

Ingredients

The formulas on this page are based on two functions: the SEQUENCE function and the MOD function.

• The SEQUENCE function is designed to create all kinds of numeric sequences. For a quick primer, watch this short video: The SEQUENCE function.
• The MOD function is a classic match formula that returns the remainder after division. MOD often shows up in problems that have a "repeating" element: highlight every other row, sum every nth row, and so on.

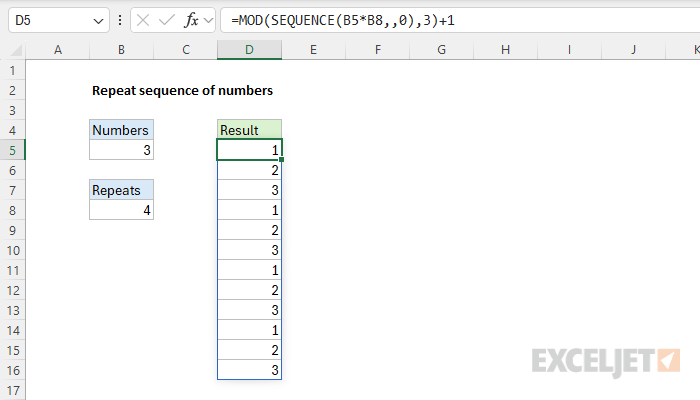
Repeat sequence of numbers

To repeat a sequence of numbers, you can use a generalized version of a formula that looks like this, where "n" is the number of items being repeated and "x" is the number of times to repeat the items:

=MOD(SEQUENCE(n*x)-1,n)+1

For example, to repeat the numbers {1,2,3} four times, n=3 and x=4, so we can use:

=MOD(SEQUENCE(3*4,,0),3)+1

What's going on here?

In a nutshell, the SEQUENCE function creates an array of sequential numbers, and the MOD function converts these numbers into repeating numbers. Working from the inside out, SEQUENCE is configured like this:

=SEQUENCE(3*4,,0)

• rows - numbers (3) * repeats (4) = 12
• columns - left blank intentionally (defaults to 1)
• start - given as 0 to start the sequence at zero instead of 1

Note that we get 12 for rows by multiplying the repeating numbers (3) by the number of repeats (4). Also note that the optional third argument, start, is given as zero to begin the sequence at 0 instead of 1. The evaluation of SEQUENCE works like this:

=SEQUENCE(3*4,,0)
=SEQUENCE(12,,0)
={0;1;2;3;4;5;6;7;8;9;10;11}

The final result is a zero-based sequence of 12 numbers. Next, the array returned by SEQUENCE is passed into the MOD function as the number argument, with the divisor set to 3:

=MOD({0;1;2;3;4;5;6;7;8;9;10;11},3)+1

The MOD function divides each number by 3 and returns the remainder after division. The result is an array of repeating numbers like this:

={0;1;2;0;1;2;0;1;2;0;1;2}+1

Finally, 1 is added to each number in the array to shift the numbers into their final form. The final result looks like this:

{1;2;3;1;2;3;1;2;3;1;2;3}

Now, let's adjust the formula to repeat the numbers 1-6 two times. For this problem, n=6 and x=2, so the formula looks like this:

=MOD(SEQUENCE(6*2,,0),6)+1

 As before, SEQUENCE generates an array of 12 numbers starting with zero, and MOD returns the remainder after dividing by 6.

=MOD(SEQUENCE(6*2,,0),6)+1
=MOD(SEQUENCE(12,,0),6)+1
=MOD({0;1;2;3;4;5;6;7;8;9;10;11},6)+1
={0;1;2;3;4;5;0;1;2;3;4;5}+1
{1;2;3;4;5;6;1;2;3;4;5;6}

In the final step, we add 1 to each number in the array to the repeating numbers from {0,1,2} to {1,2,3}. The workbook below shows how the formulas compare side-by-side:

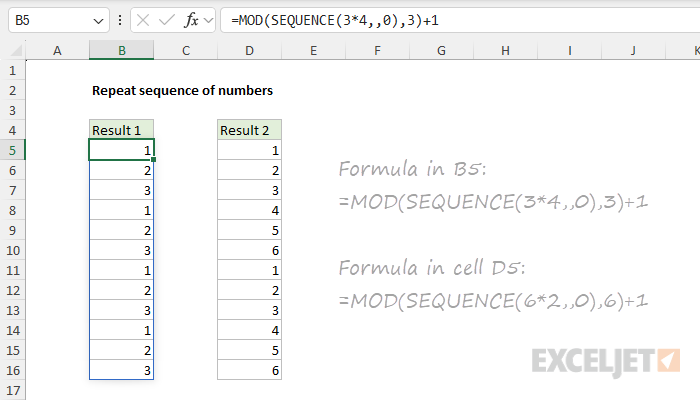
To recap, the first formula repeats the numbers 1-3 four times, and the second formula repeats the numbers 1-6 twice.

Repeat a sequence of numbers into columns

With a small adjustment, you can repeat a series of numbers in columns instead of rows. In the worksheet below, the formulas in cell B5 and cell B8 are:

B5=MOD(SEQUENCE(,3*4,0),3)+1
B8=MOD(SEQUENCE(,6*2,0),6)+1

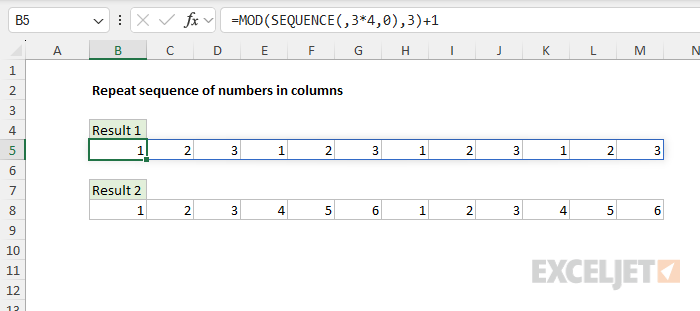
As above, the first formula repeats the numbers {1,2,3} four times, and the second formula repeats the numbers {1,2,3,4,5,6} two times. The only difference is that the n * x calculation appears as the columns argument in SEQUENCE instead of the rows argument, which is left empty.