Excel formula: Position of first partial match

Generic formula

=MATCH("*text*",rng,0)

Explanation

To get the position of the first partial match (i.e. the cell that contains text you are looking for) you can use the MATCH function with wildcards.

In the example shown, the formula in E8 is:

=MATCH("*"&E7&"*",B6:B11,0)

How this formula works

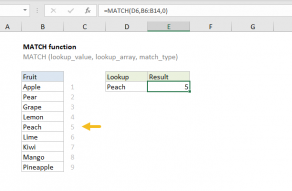
The MATCH function returns the position or "index" of the first match based on a lookup value in a range.

MATCH supports wildcard matching with an asterisk "*" (one or more characters) or a question mark "?" (one character), but only when the third argument, match_type, is set to FALSE or zero.

In the example, we pick up the value in cell E7 and use concatenation to combine this value with asterisks (*) on either side. The lookup array is the range B6 to B11, and match_type is set to zero to all partial matching with wildcards.

The result is the position of the first cell in the lookup range that contains the text "apple".

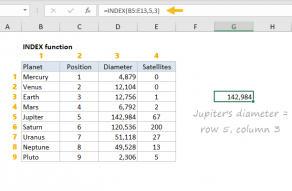
To retrieve the value of a cell at a certain position, use the INDEX function.

Author

Dave Bruns

Related formulas

Partial match against numbers with wildcard

To perform a partial match (a substring match) against numbers, you can use an array formula based on MATCH and TEXT. Background Excel supports the wildcard characters "*" and "?". However, if you use wildcards with a number, you'll convert the...

Partial match with VLOOKUP

If you want to retrieve information from a table based on a partial match, you can do so using VLOOKUP in exact match mode, and wildcards . In the example shown, the VLOOKUP formula looks like this: = VLOOKUP ( val & "*" , data , 2 ,...

Related functions

Excel MATCH Function

MATCH is an Excel function used to locate the position of a lookup value in a row, column, or table. MATCH supports approximate and exact matching, and wildcards (* ?) for partial matches. Often, the INDEX...

Excel INDEX Function

The Excel INDEX function returns the value at a given position in a range or array. You can use index to retrieve individual values or entire rows and columns. INDEX is often used with the MATCH function, where MATCH locates and feeds a position to...

Excel Formula Training

Formulas are the key to getting things done in Excel. In this accelerated training, you'll learn how to use formulas to manipulate text, work with dates and times, lookup values with VLOOKUP and INDEX & MATCH, count and sum with criteria, dynamically rank values, and create dynamic ranges. You'll also learn how to troubleshoot, trace errors, and fix problems. Instant access. See details here.