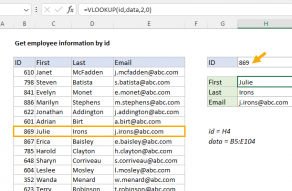
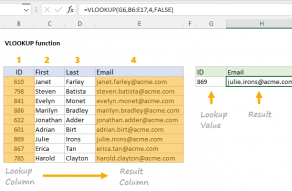
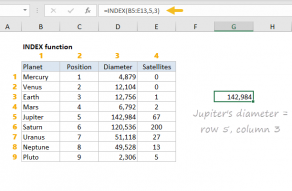
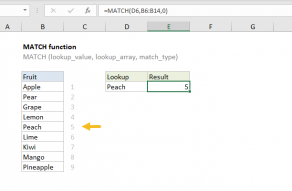
Explanation
This formula relies on a table with columns for both the full state name and the 2-letter abbreviation. Because we are using VLOOKUP, the full name must be in the first column. For simplicity, the table has been named "states".
VLOOKUP is configured to get the lookup value from column C. The table array is the named range "states", the column index is 2, to retrieve the abbreviation from the second column). The final argument, range_lookup, has been set to zero (FALSE) to force an exact match.
=VLOOKUP(C5,states,2,0)
VLOOKUP locates the matching entry in the "states" table, and returns the corresponding 2-letter abbreviation.
Generic mapping
This is a good example of how VLOOKUP can be used to convert values using a lookup table. This same approach can be used to lookup and convert many other types of values. For example, you could use VLOOKUP to map numeric error codes to human readable names.
Reverse lookup
What if you have a state abbreviation, and want to lookup the full state name using the lookup table in the example? In that case, you'll need to switch to INDEX and MATCH. With a lookup value in A1, this formula will return a full state name with the lookup table as shown:
=INDEX(G5:G55,MATCH(A1,H5:H55,0))
If you want to use the same named range "states" you can use this version to convert a 2-letter abbreviation to a full state name.
=INDEX(INDEX(states,0,1),MATCH(A1,INDEX(states,0,2),0))
Here, we use INDEX to return whole columns by supplying a row number of zero. This is a cool and useful feature of the INDEX function: if you supply zero for row, you get whole column(s) if you supply zero for column, you get whole row(s).