CSC Function

The CSC function returns the cosecant of an angle provided in radians. In geometric terms, the cosecant of an angle is equal to the ratio of a right triangle's hypotenuse divided by its opposite side. For example, the cosecant of PI()/6 or 30° returns the ratio 2.0.

=CSC(PI()/6) // Returns 2.0

Using Degrees

The CSC function expects radians. To supply an angle to CSC in degrees, multiply the angle by PI()/180 or use the RADIANS function to convert to radians. For example, to get the CSC of 60 degrees, you can use either formula below:

=CSC(60*PI()/180)
=CSC(RADIANS(60))

Explanation

The graph of cosecant, shown above, visualizes the output of the function for angles from 0 to a full rotation. The function has vertical asymptotes within the range  [0, 2π] at the points 0, π and 2π where the output diverges to infinity. CSC is the inverse of SIN and can be equivalently defined in the formula below:

=CSC(angle)=1/SIN(angle)

The relationship between cosecant and sine is visualized by the graph of the two functions shown below:

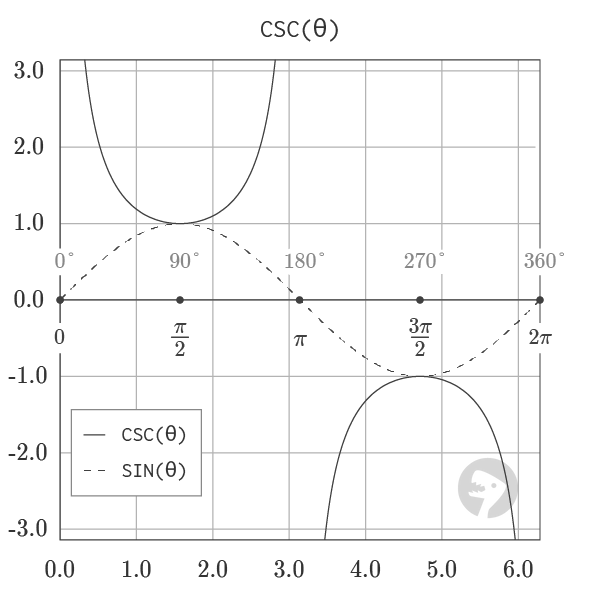
Graphs courtesy of wumbo.net.